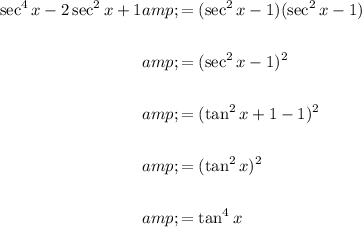Question

Verify that the following is an identity. sec^4 x - 2 sec^4 x + 1 = tan^4 x

Answer 1

See below.

Explanation:

Given trigonometric equation:

`\sec^4x-2\sec^2x+1=\tan^4x`

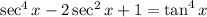
To verify the given equation, we can manipulate the left side until it equals the right side.

Begin by factoring the left side using the substitution u = sec²x.

If u = sec²x then u² = sec⁴x so:

`\sec^4x-2\sec^2x+1=u^2-2u+1`

Factor the quadratic:

`\begin{aligned}u^2-2u+1&=u^2-u-u+1\\&=u(u-1)-1(u-1)\\&=(u-1)(u-1)\\&=(u-1)^2\end{aligned}`

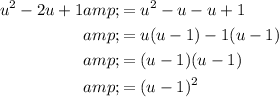
Now, substitute back in u = sec²x, so:

`\sec^4x-2\sec^2x+1=(\sec^2x-1)^2`

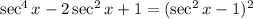
The Pythagorean identity states that sec²x = tan²x + 1, so substitute this:

`=(\tan^2x+1-1)^2`

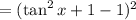
Finally, simplify:

`=(\tan^2x)^2\\\\\\=\tan^4x`

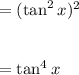
Therefore, we have verified that:

`\sec^4x-2\sec^2x+1=\tan^4x`

`\hrulefill`

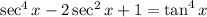
As one calculation:

`\begin{aligned}\sec^4x-2\sec^2x+1&=(\sec^2x-1)(\sec^2x-1)\\\\&=(\sec^2x-1)^2\\\\&=(\tan^2x+1-1)^2\\\\&=(\tan^2x)^2\\\\&=\tan^4x\end{aligned}`