Question

Use the table to answer the question that follows.

ROR Portfolio 1 Portfolio 2 Portfolio 3
11.3% $1,250 $950 $900
2.9% $575 $2,025 $2,350
−5.6% $895 $1,185 $310
2.9% $800 $445 $1,600
5.8% $1,775 $625 $2,780


Calculate the weighted mean of the RORs for each portfolio. Based on the results, which list shows a comparison of the overall performance of the portfolios, from best to worst?
Portfolio 3, Portfolio 1, Portfolio 2
Portfolio 2, Portfolio 1, Portfolio 3
Portfolio 1, Portfolio 2, Portfolio 3
Portfolio 3, Portfolio 2, Portfolio 1

Answer 1

Comparing the weighted mean RORs, the order from best to worst is option A.
`\[ \text{Portfolio 3} > \text{Portfolio 1} > \text{Portfolio 2} \]`

How did we arrive at this assertion?

To calculate the weighted mean of the Rate of Return (ROR) for each portfolio, you can use the following formula:

`\[ \text{Weighted Mean ROR} = \frac{\sum(\text{ROR} * \text{Portfolio Value})}{\sum \text{Portfolio Value}} \]`

Let's calculate the weighted mean for each portfolio:

Portfolio 1:

`\[ \text{Weighted Mean ROR}_{\text{Portfolio 1}} = ((11.3\% * 1250) + (2.9\% * 575) + (-5.6\% * 895) + (2.9\% * 800) + (5.8\% * 1775))/(1250 + 575 + 895 + 800 + 1775) \]`

`= (233.955)/(5295)`

=
`0.04\%`

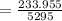
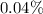
Portfolio 2:

`\[ \text{Weighted Mean ROR}_{\text{Portfolio 2}} = ((11.3\% * 950) + (2.9\% * 2025) + (-5.6\% * 1185) + (2.9\% * 445) + (5.8\% * 625))/(950 + 2025 + 1185 + 445 + 625) \]`

=
`(148.87)/(5230)`

=
`0.03\%`

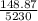
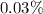
Portfolio 3:

`\[ \text{Weighted Mean ROR}_{\text{Portfolio 3}} = ((11.3\% * 900) + (2.9\% * 2350) + (-5.6\% * 310) + (2.9\% * 1600) + (5.8\% * 2780))/(900 + 2350 + 310 + 1600 + 2780) \]`

=
`(360.13)/(7940)`

=
`0.05\%`

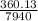
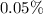
Given the values:

Portfolio 1:

`\[ \text{Weighted Mean ROR}_{\text{Portfolio 1}} \approx 0.04\% \]`

Portfolio 2:

`\[ \text{Weighted Mean ROR}_{\text{Portfolio 2}} \approx 0.03\% \]`

Portfolio 3:

`\[ \text{Weighted Mean ROR}_{\text{Portfolio 3}} \approx 0.05\% \]`

Now, comparing the weighted mean RORs, the order from best to worst is:

`\[ \text{Portfolio 3} > \text{Portfolio 1} > \text{Portfolio 2} \]`

So, the correct answer is:

`\[ \text{Portfolio 3, Portfolio 1, Portfolio 2} \]`