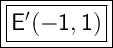Question

The point E(1, -1) is reflected over the line y = x. What are the coordinates of the resulting point, E'?​

Answer 1

E(-1, 1)

Explanation:

A reflection is a transformation in which a geometric figure or object is flipped over a line, creating a mirror image with respect to that line.

When a point is reflected over the line y = x, the x and y coordinates are swapped.

Therefore, the mapping rule for a reflection in the line y = x is:

`\large\boxed{\begin{array}{c}\underline{\textsf{Reflection in the line $y=x$}}\\\\(x,y) \rightarrow (y, x)\end{array}}`

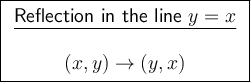
To reflect point E(1, -1) in the line y - x, all we need to do is swap the coordinates. Therefore, the coordinates of point E' are:

`\Large\boxed{\boxed{\sf E'(-1,1)}}`