Amber's post travels the fastest. This is shown in the equation form of the functions by comparing the coefficients and bases. The function with the largest growth rate will lead to the post traveling the fastest.
To determine which student's post travels the fastest, we can look at the function that represents the number of shares each day.
The function for Amber's post is
, where x represents the number of days.
The function for Ben's post is
, and the function for Carter's post is
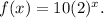
By comparing the growth of these functions, we can see that the function with the largest growth rate will lead to the post traveling the fastest.
In this case, the function
has the largest growth rate because the base of the exponential function (4) is greater than the bases of the other functions (3 and 2).
Therefore, Amber's post travels the fastest.
This is shown in the equation form of the functions by observing the coefficients and bases.
The coefficient represents the initial number of shares, and the base represents the rate of growth.
The larger the base, the faster the number of shares will increase over time.
The probable question may be:
Three Algebra 1 students are comparing how fast their social media posts have spread. Their results are shown in the following table: Student Amber Ben Carter Description Amber shared her photo with 3 people. They continued to share it, so the Ben shared his post with 2 friends. Each of those friends shares with 3 more share with only 2 people each day. Carter shared his post with 10 friends, who ea number of shares increases every day, as shown by the function. every day, so the number of shares triples every day. Social Media Post f(x)=3(4)^x Day Number of Shares Carter shared his post with 10 friends, who Shares 0 2 each share with only 2 people each day. 1 6 2 18
Based on your results, which students' post travels the fastest? How is this shown in the equation form of the functions?