The equation of any line perpendicular to these parallel lines is:
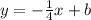 , where b is any constant.
, where b is any constant.
The slope of the parallel lines is 4, so the slope of the perpendicular line is its negative reciprocal, which is
 .
.
To find the value of b, we can use the point-slope form of linear equations:
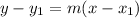
where m is the slope of the line and
 is a point on the line.
is a point on the line.
Let's choose the point (0, 1) on the perpendicular line. Substituting these values into the equation above, we get:
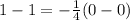
0 = 0
This is a true statement, so our equation is correct.
Therefore, any line perpendicular to the parallel lines in the image has the equation:
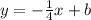
where b is any constant.