Question

In a laboratory experiment, a student is asked to remove a hair from her head. The single hair is then taped to the emitting end of a helium-neon laser, which operates at a wavelength of = 632.8 nm. A diffraction pattern is observed on a wall that is x = 1.9 m from the end of the laser. The distance between the m = −8 and 8 minima is measured to be y = 19.0 cm. What is the width a of this human hair? For comparison, the typical width of a human hair is 50 µm.

Answer 1

The width of the human hair can be found using the formula for the double-slit interference pattern and the given values. The width of the hair is approximately 75.2 μm.

Step-by-step explanation:

To find the width a of the human hair, we need to use the formula for the double-slit interference pattern:

d*sin(θ) = m*λ

Where d is the distance between the slits, θ is the angle to the mth order maximum, and λ is the wavelength of the light. In this case, λ is given as 632.8 nm and θ can be calculated using the distance between the wall and the laser tape.

The width of the hair can then be found by rearranging the formula:

a = (m*λ*L)/(d*sin(θ))

Using the given values, we can substitute them into the formula to find the width of the hair.

`a = (8*(632.8*10^-^9 m)*(1.9 m))/(19*10^-^3 m)`

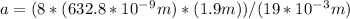
≈ 75.2 μm