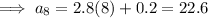Answer:
22.6
Explanation:
Given:
Find the value of a₆:
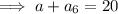
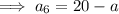
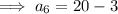
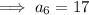
Therefore:
General form of an arithmetic sequence:
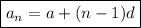
Where:
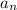 is the nth term.
is the nth term.- a is the first term.
- d is the common difference between terms.
- n is the position of the term.
Substitute a = 3 and a₆ = 17 into the formula and solve for d:
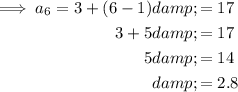
Therefore, the equation for the nth term is:
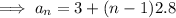
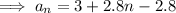
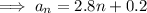
To find the 8th term, substitute n = 8 into the equation for the nth term: