Question

The count in a bacteria culture was 800 after 20 minutes and 1900 after 40 minutes. Assuming the count grows exponentially,

What was the initial size of the culture

______bacteria

Find the doubling period.

______minutes

Find the population after 100 minutes.

_____ bacteria

When will the population reach 15000.

____ minutes

Answer 1

Initial size = 337 bacteria

Doubling period = 16 minutes

Population after 100 minutes = 25453 bacteria

Population 15000 = 88 minutes

(NB Please see "Additional Notes" at the end of the explanation)

Explanation:

The general form of a population growth function is:

`\boxed{\begin{array}{l}\underline{\textsf{General form of a Population Growth Function}}\\\\\large\text{$P(t)=P_0\cdot e^(kt)$}\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$P(t)$ is the total population after time $t$.}\\\phantom{ww}\bullet\;\textsf{$P_0$ is the initial population.}\\\phantom{ww}\bullet\;\textsf{$k$ is the growth rate.}\\\phantom{ww}\bullet\;\textsf{$t$ is time.}\end{array}}`

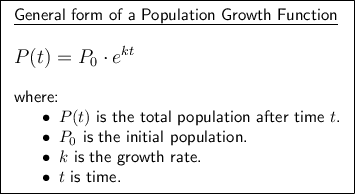
Given that the count in a bacteria culture was 800 after 20 minutes and 1900 after 40 minutes, then:

`P(20) = 800`

`P(40) = 1900`

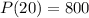
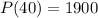
Substitute these values into the function:

`800=P_0 \cdot e^(20k)`

`1900=P_0 \cdot e^(40k)`

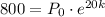
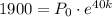
Divide the second equation by the first to eliminate P₀ and solve for k:

`(P_0 \cdot e^(40k))/(P_0 \cdot e^(20k))=(1900)/(800)`

`(e^(40k))/(e^(20k))=(19)/(8)`

`e^(40k-20k)=(19)/(8)`

`e^(20k)=(19)/(8)`

`\ln\left(e^(20k)\right)=\ln\left((19)/(8)\right)`

`20k\ln\left(e\right)=\ln\left((19)/(8)\right)`

`20k=\ln\left((19)/(8)\right)`

`k=(1)/(20)\ln\left((19)/(8)\right)`

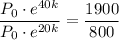
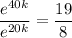
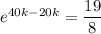
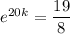
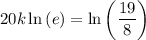
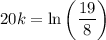
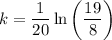
Now, substitute P(20) = 800 and the found value of k into the general function and solve for P₀:

`P_0 \cdot e^{20\cdot (1)/(20)\ln\left((19)/(8)\right)}=800`

`P_0 \cdot e^{\ln\left((19)/(8)\right)}=800`

`P_0 \cdot \left((19)/(8)\right)=800`

`P_0 =800\cdot \left((8)/(19)\right)`

`P_0 =(6400)/(19)`

`P_0 =336.84210526...`

`P_0 \approx337`

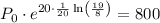
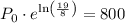
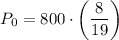
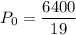
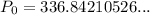
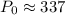
Therefore, the initial size of the culture was approximately 337 bacteria (rounded to the nearest whole number).

`\hrulefill`

To find the doubling period, substitute the found value of k, P₀ = 1 and P(t) = 2 into the general function and solve for t:

`1 \cdot e^{(t)/(20)\ln\left((19)/(8)\right)}=2`

`e^{(t)/(20)\ln\left((19)/(8)\right)}=2`

`\left( e^{\ln\left((19)/(8)\right)}\right)^{(t)/(20)}=2`

`\left( (19)/(8)\right)^{(t)/(20)}=2`

`\left(\left( (19)/(8)\right)^{(1)/(20)}\right)^t=2`

`\ln\left(\left( (19)/(8)\right)^{(1)/(20)}\right)^t=\ln2`

`t\ln\left(\left( (19)/(8)\right)^{(1)/(20)}\right)=\ln2`

`t=\frac{\ln2}{\ln\left(\left( (19)/(8)\right)^{(1)/(20)}\right)}`

`t=16.0265718...`

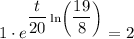
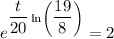
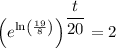
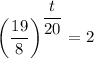
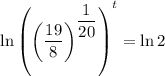
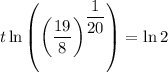
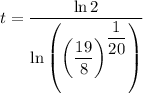
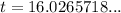
Therefore, the doubling period is 16 minutes (rounded to the nearest minute).

`\hrulefill`

The function that models the count in bacteria culture P(t) after t minutes is:

`\Large\boxed{P(t)=\left((6400)/(19)\right)\cdot e^{(t)/(20)\ln\left((19)/(8)\right)}}`

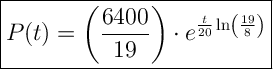
To find the population after 100 minutes, substitute t = 100 into the function:

`P(100)=\left((6400)/(19)\right)\cdot e^{(100)/(20)\ln\left((19)/(8)\right)}`

`P(100)=25453.3203...`

`P(100)=25453`

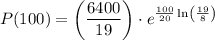
Therefore, the population after 100 minutes is 25453 bacteria (rounded to the nearest whole number).

`\hrulefill`

To find when the population will reach 15000, substitute P(t) = 15000 into the function and solve for t:

`\left((6400)/(19)\right)\cdot e^{(t)/(20)\ln\left((19)/(8)\right)}=15000`

`e^{(t)/(20)\ln\left((19)/(8)\right)}=(1425)/(32)`

`\left(e^\ln\left((19)/(8)\right)}\right)^{(t)/(20)}=(1425)/(32)`

`\left((19)/(8)\right)^{(t)/(20)}=(1425)/(32)`

`\left(\left((19)/(8)\right)^{(1)/(20)}\right)^t=(1425)/(32)`

`\ln\left(\left((19)/(8)\right)^{(1)/(20)}\right)^t=\ln\left((1425)/(32)\right)`

`t\ln\left(\left((19)/(8)\right)^{(1)/(20)}\right)=\ln\left((1425)/(32)\right)`

`t=\frac{\ln\left((1425)/(32)\right)}{\ln\left(\left((19)/(8)\right)^{(1)/(20)}\right)}`

`t=87.7734667...`

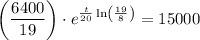
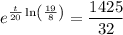
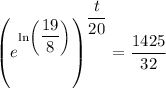
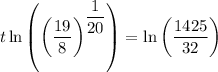
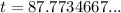
Therefore, the population will reach 15000 after 87 minutes and 46 seconds, or 88 minutes rounded to the nearest minute.

`\hrulefill`

Additional notes

I have used the exact values of (P₀) and k throughout the calculations for accuracy. However, it is often acceptable to round them to 3 significant figures. In this case, the function would be:

`\Large\boxed{P(t)=337\cdot e^(0.0432t)}`

If you do use this rounded function, it will give the same answers for all questions except the population after 100 minutes.

When using the rounded function, the population after 100 minutes is 25339.

The attached graph is for the function using the exact values of (P₀) and k. I have shown the point when P(t) = 1600 to confirm that the doubling period is 16 minutes.