Question

For the years from 2001-2010, the number of Americans traveling to other countries by plane can be represented by the polynomial function A(t)= 20t ^ 4 - 428t ^ 3 + 2760t ^ 2 -; 4320t + 33600 where A is the number of thousands of Americans traveling abroad by airplane and t is the number of years since 2001. In which year were there 40,000.000 Americans traveling abroad? Use the Rational Root Theorem to find your answer. I factored by 4.

Answer 1

Using the Rational Root Theorem, we can test different values of t to find a root that satisfies the equation. By testing values, we find that t = 2 is a root of the equation, so in the second year after 2001, there were 40,000,000 Americans traveling abroad. Therefore, the year when there were 40,000,000 Americans traveling abroad is 2003.

To find the year when there were 40,000,000 Americans traveling abroad, we need to set the polynomial function A(t) equal to 40,000. To do this, we can rearrange the equation and set it equal to 0:

20
`t^4` - 428
`t^3` + 2760
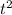`t^2` - 4320t + 33600 = 40,000

This equation can be solved using the Rational Root Theorem which states that any rational root of a polynomial equation is in the form p/q, where p is a factor of the constant term (33600) and q is a factor of the leading coefficient (20). By testing different values of p and q, we can find the value of t that satisfies the equation. Once we find the value of t, we can add it to 2001 to determine the year.

Using the Rational Root Theorem, we can test values such as ±1, ±2, ±3, etc. to find a root that satisfies the equation. By testing these values, we find that t = 2 is a root of the equation. Therefore, in the second year after 2001, there were 40,000,000 Americans traveling abroad. Therefore, the year when there were 40,000,000 Americans traveling abroad is 2003.