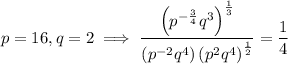Question

please help ASAP, ty! (this is 50 points too) Directions: Simplify the following expressions. Show your solution and box your final answer.​

Answer 1

`\textsf{1)} \quad 27^{(1)/(3)}=3`

`\textsf{2)} \quad \left((1)/(343)\right)^{-(2)/(3)}=49`

`\textsf{3)} \quad 6y^{(1)/(2)}\cdot y^{(4)/(3)}=6y^{(11)/(6)}`

`\textsf{4)} \quad \frac{32c^2}{4c^{(1)/(2)}}=8c^{(3)/(2)}`

`\textsf{5)} \quad p=16, q=2 \implies \frac{\left(p^{-(3)/(4)}q^(3)\right)^{(1)/(3)}}{\left(p^(-2)q^(4)\right)\left(p^(2)q^(4)\right)^{(1)/(2)}}=(1)/(4)`

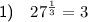
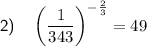
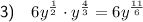
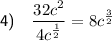
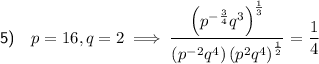
Explanation:

To simplify the given expressions, we can use exponent rules:

`\boxed{\begin{array}{rl}\underline{\sf Exponent\;Rules}\\\\\sf Product:&a^m * a^n=a^(m+n)\\\\\sf Quotient:&a^m / a^n=a^(m-n)\\\\\sf Power\;of\;a\;Power:&(a^m)^n=a^(mn)\\\\\sf Power\;of\;a\;Product:&(ab)^m=a^mb^m\\\\\sf Negative\;Exponent:&a^(-m)=(1)/(a^m)\\\\\end{array}}`

`\hrulefill`

Question 1

To simplify the given expression, begin by expressing 27 as the product of primes.

Since 27 = 3 × 3 × 3, the prime factorization of 27 is 3³:

`27^{(1)/(3)}=\left(3^3\right)^{(1)/(3)}`

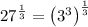
Now, apply the power of a power exponent rule:

`3^{\left(3 \cdot(1)/(3)\right)}=3^{(3)/(3)}=3^1=3`

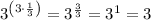
Therefore:

`27^{(1)/(3)}=3`

`\hrulefill`

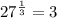
Question 2

To simplify the given expression, begin by expressing 343 as the product of primes.

Since 343 = 7 × 7 × 7, the prime factorization of 343 is 7³:

`\left((1)/(343)\right)^{-(2)/(3)}=\left((1)/(7^3)\right)^{-(2)/(3)}`

Now, apply the negative exponent rule:

`=\left(7^(-3)\right)^{-(2)/(3)}`

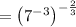
Finally, apply the power of a power exponent rule, then simplify:

`\begin{aligned}&=7^{\left(-3\cdot-(2)/(3)\right)}\\\\&=7^{\left((6)/(3)\right)}\\\\&=7^2\\\\&=49\end{aligned}`

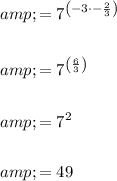
Therefore:

`\left((1)/(343)\right)^{-(2)/(3)}=49`

`\hrulefill`

Question 3

To simplify the given expression, apply the product exponent rule:

`\begin{aligned}6y^{(1)/(2)}\cdot y^{(4)/(3)}&=6y^{\left((1)/(2)+(4)/(3)\right)}\\\\&=6y^{\left((3)/(6)+(8)/(6)\right)}\\\\&=6y^{(11)/(6)}\end{aligned}`

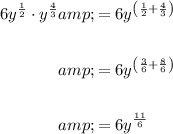
Therefore:

`6y^{(1)/(2)}\cdot y^{(4)/(3)}=6y^{(11)/(6)}`

`\hrulefill`

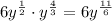
Question 4

To simplify the given expression, begin by dividing the numbers 32 and 4:

`\frac{32c^2}{4c^{(1)/(2)}}=\frac{8c^2}{c^{(1)/(2)}}`

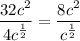
Now, apply the quotient rule:

`\begin{aligned}&=8c^{\left(2-(1)/(2)\right)}\\\\&=8c^{(3)/(2)}\end{aligned}`

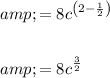
Therefore:

`\frac{32c^2}{4c^{(1)/(2)}}=8c^{(3)/(2)}`

`\hrulefill`

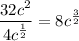
Question 5

Given expression:

`\frac{\left(p^{-(3)/(4)}q^(3)\right)^{(1)/(3)}}{\left(p^(-2)q^(4)\right)\left(p^(2)q^(4)\right)^{(1)/(2)}}`

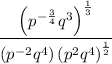
Before evaluating the expression when p = 16 and q = 2, we will simplify the expression.

Begin by applying the power of a power exponent rule:

`\begin{aligned}(\left(p^(-\frac34)q^3\right)^(\frac13))/(\left(p^(-2)q^4\right)\left(p^2q^4\right)^(\frac12))&=(\left(p^(-\frac34)\right)^(\frac13)\cdot(q^3)^(\frac13))/((p^(-2)q^4)\cdot(p^2)^(\frac12)\cdot (q^4)^(\frac12))\\\\&=(p^(\left(-\frac34\cdot\frac13\right))\cdot q^(\left(3\cdot \frac13\right)))/((p^(-2)q^4)\cdot p^(\left(2\cdot \frac12\right))\cdot q^(\left(4\cdot \frac12\right)))\\\\&=(p^(-\frac14)\cdot q^1)/((p^(-2)q^4)\cdot p^1\cdot q^2)\end{aligned}`

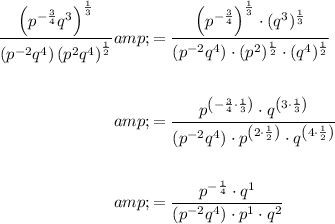
Now, apply the product exponent rule to the denominator:

`\begin{aligned}&=(p^(-\frac14)\cdot q^1)/(p^(-2)\cdot q^4 \cdot p^1 \cdot q^2)\\\\&=(p^(-\frac14)\cdot q^1)/(p^(-2)\cdot p^1 \cdot q^4 \cdot q^2)\\\\&=(p^(-\frac14)\cdot q^1)/(p^((-2+1)) \cdot q^((4+2)))\\\\&=(p^(-\frac14)\cdot q^1)/(p^(-1) \cdot q^(6))\end{aligned}`

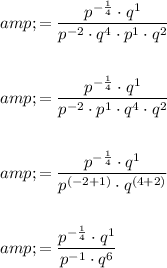
Next, apply the quotient exponent rule:

`\begin{aligned}&=p^(\left(-\frac14-(-1)\right))\cdot q^((1-6))\\\\&=p^(\frac34)\cdot q^(-5)\end{aligned}`

Finally, apply the negative exponent rule:

`=(p^(\frac34))/(q^5)`

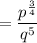
Now we have simplified the given expression, we can substitute p = 16 and q = 2:

`=(16^(\frac34))/(2^5)`

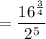
Rewrite 16 as the product of primes: 16 = 2⁴

`=((2^4)^(\frac34))/(2^5)`

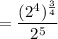
Apply the power of a power exponent rule:

`=(2^(\left(4\cdot\frac34\right)))/(2^5)\\\\\\=(2^3)/(2^5)`

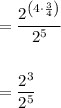
Apply the quotient power rule:

`=2^((3-5))\\\\\\=2^(-2)`

Finally, apply the negative exponent rule:

`=(1)/(2^2)\\\\\\=(1)/(4)`

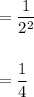
Therefore, the value of the expression when p = 16 and q = 2 is:

`p=16, q=2 \implies \frac{\left(p^{-(3)/(4)}q^(3)\right)^{(1)/(3)}}{\left(p^(-2)q^(4)\right)\left(p^(2)q^(4)\right)^{(1)/(2)}}=(1)/(4)`