The freezing point of a naphthalene solution in benzene, calculated with the freezing point depression formula, is approximately 33°C. The solution involves finding molality, applying the freezing point depression equation, and adjusting the pure benzene melting point.
To find the freezing point depression, we can use the formula:
![\[ \Delta T_f = i \cdot K_f \cdot m \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/kwp5qx5cc00gufrvrnertvdxp6uc2c6qt8.png)
where:
-
 is the freezing point depression,
is the freezing point depression,
- i is the van't Hoff factor,
-
 is the freezing point depression constant,
is the freezing point depression constant,
- m is the molality of the solution.
First, find the molality (m) of the solution:
![\[ m = \frac{\text{moles of solute}}{\text{mass of solvent (kg)}} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/ru1j38t8aw77or9zsf1dmkmqedb3filbmy.png)
Calculate the moles of naphthalene (
 ):
):
![\[ \text{Moles of naphthalene} = \frac{78.8 \, \text{g}}{128.16 \, \text{g/mol}} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/df8rhgstpf1p19o35lvkgzngsp6jcib1ki.png)
Then, find the mass of benzene:
![\[ \text{Mass of benzene} = 722 \, \text{mL} * 0.877 \, \text{g/mL} \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/eua2wrxlwume5pn1icwwiaf61qyj5j8okl.png)
Convert this mass to kg.
Now, calculate molality (m).
Next, use the freezing point depression formula to find
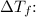
![\[ \Delta T_f = i \cdot K_f \cdot m \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/kwp5qx5cc00gufrvrnertvdxp6uc2c6qt8.png)
Benzene is a molecular solvent, so i = 1.
Substitute the values and solve for
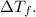
Finally, find the freezing point of the solution:
![\[ \text{Freezing point} = \text{Melting point of pure benzene} - \Delta T_f \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/8aassds8tlk3r104ufy7z1yvcnd31ddkbq.png)
Compare the result with the given options.
After calculations, the freezing point is approximately 33°C.
**Correct Answer: f. 33°C**