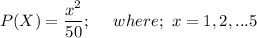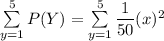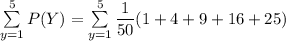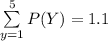Answer:
Explanation:
Given that:
P(Y) = ky
where;
y =1,2,...7
To find the value of c or k (constant)
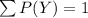
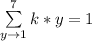
= k(1+2+3+4+5+6+7) = 1
28k = 1
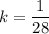
b) The required probability is P ( X ≤ 3)
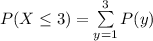
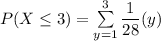
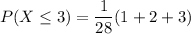
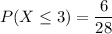
P ( X ≤ 3) = 0.2143
c) The required probability P(2 ≤ Y ≤ 4)
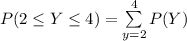
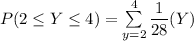
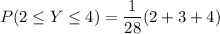
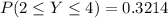
d) The required probability: