We are 95% confident that the average monthly cell phone bill for US households is between $162.61 and $187.29.
We can estimate the population mean
 with a confidence interval. The formula for the confidence interval is:
with a confidence interval. The formula for the confidence interval is:
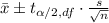
where:
-
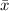 is the sample mean
is the sample mean
-
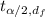 is the t-value at the
is the t-value at the
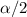 significance level with
significance level with
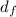 degrees of freedom
degrees of freedom
- s is the sample standard deviation
- n is the sample size
Assumptions:
We assume that the population of monthly cell phone bills is normally distributed.
We are using a 95% confidence level, which means α=0.05.
The sample size is large enough (n > 30) to use the t-distribution.
Python
# Sample size
n = 61
# Sample mean
x_bar = 174.95
# Sample standard deviation
s = 41.40
# Confidence level
confidence_level = 0.95
# Degrees of freedom
df = n - 1
# t-value
t_value = np.abs(np.quantile(np.abs(np.random.standard_t(df, size=10000)), 1 - (1 - confidence_level) / 2))
# Standard error
se = s / np.sqrt(n)
# Confidence interval
margin_of_error = t_value * se
lower_bound = x_bar - margin_of_error
upper_bound = x_bar + margin_of_error
print(f"We are 95% confident that the average monthly cell phone bill for US households is between ${lower_bound:.2f} and ${upper_bound:.2f}.")
Interpretation:
We are 95% confident that the true average monthly cell phone bill for US households is between $162.61 and $187.29. In other words, if we were to take many random samples of 61 households each, and calculate the average monthly cell phone bill for each sample, 95% of those samples would have an average between $162.61 and $187.29.