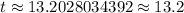Answer:
approximately 13.2 years
Explanation:
Interpreting The Question
So we start off with the general equation:
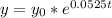 , in this exponential function, the
, in this exponential function, the
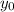 represents the initial value or the y-intercept, and when this value becomes doubled that means it's being multiplied by 2. Conveniently this value is being multiplied by:
represents the initial value or the y-intercept, and when this value becomes doubled that means it's being multiplied by 2. Conveniently this value is being multiplied by:
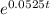 , meaning this has to be equal to two for the initial investment to double.
, meaning this has to be equal to two for the initial investment to double.
Logarithms
Logarithms are going to be super useful in these types of questions, and are essentially the inverse of an exponential.
So if I have a log in the form:
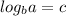 that means that "I have to raise 'b' to the power of 'c' to get the result 'a'" or in equation form:
that means that "I have to raise 'b' to the power of 'c' to get the result 'a'" or in equation form:
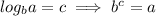
Generally we define the base 'b' to some value, but there are two logarithms that show up a lot: log which has a base of 10 and ln pronounced "natural log" which has a base of "e"
This just means that:
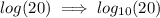 even if the base wasn't explicitly written
even if the base wasn't explicitly written
Likewise:
 even if the base wasn't explicitly written.
even if the base wasn't explicitly written.
Solving for T
we know that
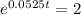
so from here let's take the natural log
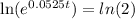
the expression
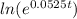 is essentially saying what do I have to raise the base "e" to the power of, to get "e^0.0525t" and we're essentially given the answer... 0.0525t is what we need to raise it to the power of, so that's what it simplifies to
is essentially saying what do I have to raise the base "e" to the power of, to get "e^0.0525t" and we're essentially given the answer... 0.0525t is what we need to raise it to the power of, so that's what it simplifies to
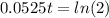
from here divide both sides by 0.0525
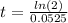
now approximate natural log using a calculator
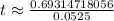
now approximate this using a calculator once more