Question

The profit function P(x) is the revenue function R(x) (how much it takes in) minus the cost function C(x) (how much it spends). In economic models, one typically assumes that a company wants to maximize its profit, or at least make a profit!

Part A: Answer the following questions about the cost function C(2) and the revenue function R(x).
1. What is the domain and range of C (x)?
2. What is the meaning of the slope and intercept of C(x)?
3. At what production level 2 will the company receive the most revenue?
Part B. Answer the following questions about the profit function P(x).
4. Assuming that the company sells all that it produces, what is the profit function?
5. Why is finding the range of P(x) important?
6. The company can choose to produce either 60 or 70 items. What is their profit for each case, and which level of production should they choose?
7. Can you explain, from our model, why the company makes less profit when producing 10 more units?

Answer 1

a).

1. The domain of C(x)

`$x \in [0, \infty)$`

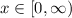
Range of c(x) is
`$[0, \infty)$`

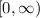
Since the negative value do not make any sense.

2. C(x) = Ax + b

Intercept here denotes the fixed cost (that is when x = 0)

The slope indicates the marginal cost (that is increase in cost per unit of quantity)

3. Revenue is maximum marginal revenue = 0

(that is when at the top of the parabola)

4. Profit = R(x) -C(x)

5. Range of P(x) is important so that we have the idea in mind about the maximum loss and the maximum profit for a particular quantity.

6 and 7 -- insufficient data.