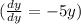Answer:
The responses to this questin can be defined as follows:
Explanation:
Take system A. The predator must be there. If we feel the attacker is x, that drop in y (a further prey eaten) must raise by x. Growing x could render y falling much quicker because more predators become available. See the equation of
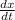 .
.
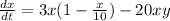
It will see that dx/dt is an x both y function. It is indeed difficult to tell something about the dependence among
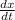 and x, but it is quite easy: the higher to y, its higher the 20xy (since x and y are positive numbers). And therefore -20xy is much more negative, but
and x, but it is quite easy: the higher to y, its higher the 20xy (since x and y are positive numbers). And therefore -20xy is much more negative, but
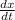 is much worse. Going to find: the larger y, the less or even more negative
is much worse. Going to find: the larger y, the less or even more negative
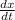 , the less x.
, the less x.
Test: It implies that higher y means less x (more prey) (fewer predators). Then, does the assumption which x is a predator confirmed? No, because more prey, and thus more predators, would mean better lunch for both the predators, People could see that x is now a prey as well as y a predator, even though more predators(y) exist.
They use the second equation to check this:
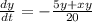
Perhaps, now we're just talking about basic dependency as of now: one is from dy/dt to x. A larger x means that the y (predator) is growing faster. For System B we are using the same rationale.Thus, x is a predator and y a predator (as high x indicates higher 25 x but this results in increased y population increase (EQ.2), as higher x means lower
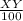 and reduces x) Afterwards, we would like to learn which system has big and small predators. To conclusion, they must realize that this piranha does not impact that population of humans in the case of piranhas. However in cases where y = I and y = i+1 would not significantly differ from
and reduces x) Afterwards, we would like to learn which system has big and small predators. To conclusion, they must realize that this piranha does not impact that population of humans in the case of piranhas. However in cases where y = I and y = i+1 would not significantly differ from
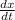 (alter in the number of individuals) (i is an arbitrary number of piranhas)
(alter in the number of individuals) (i is an arbitrary number of piranhas)
This function of system B can be seen:
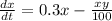 . And what's the reason? Given the fact that the element beside y is
. And what's the reason? Given the fact that the element beside y is
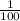 , another tiger shark is no worse than
, another tiger shark is no worse than
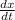 and therefore not willing to make a significant contribution to the elimination of global life. Through system A, they could see that the predator is huge because one predator implies a major shift in
and therefore not willing to make a significant contribution to the elimination of global life. Through system A, they could see that the predator is huge because one predator implies a major shift in
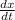 almost. I belive that, this message has been observed by you. But I also hope that throughout the end I have created no error:) This should try to not learn with your heart, since it is helpful when you grasp the task. Another way to approach the problem might be to try to consider
almost. I belive that, this message has been observed by you. But I also hope that throughout the end I have created no error:) This should try to not learn with your heart, since it is helpful when you grasp the task. Another way to approach the problem might be to try to consider
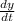 instead of
instead of
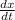 for both systems and then to see that what prey is tiny or large. This big predator should not imply many hunters with one location or each other and will eat a meal (System A seems to have this feature:
for both systems and then to see that what prey is tiny or large. This big predator should not imply many hunters with one location or each other and will eat a meal (System A seems to have this feature: