Answer:
(a):
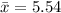 and
and
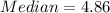
(b):
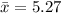 and
and
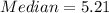
(c): New York Yankees
Explanation:
Given
Data of New York ERA and Baltimore ERA
Solving (a): Mean and Median of New York ERA
Mean is calculated as:
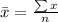
For New York ERA, n = 19. So, we have:
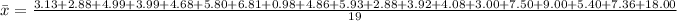
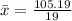
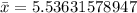
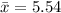
To calculate the median value, we first arrange the data (in ascending order):
So, we have:
0.98, 2.88, 2.88, 3.00, 3.13, 3.92, 3.99, 4.08, 4.68, 4.86, 4.99, 5.40, 5.80, 5.93, 6.81, 7.50, 7.36, 9.00, 18.00
The median value of odd number of data is:
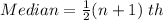
Substitute 19 for n
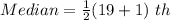
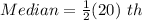
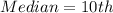
So, the median is the 10th item.
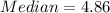
(b): Mean and Median of Baltimore ERA
Mean is calculated as:
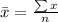
For Baltimore ERA, n = 17. So, we have:
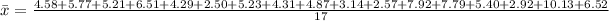
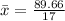
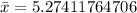
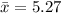 --- approximated
--- approximated
Arrange in ascending order:
2.50 , 2.57 , 2.92 , 3.14 , 4.29 , 4.31 , 4.58 , 4.87 , 5.21, 5.23 , 5.40 ,5.77 , 6.51 , 6.52, 7.79 , 7.92 , 10.13
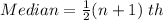
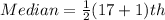
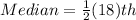
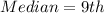
So, the median is the 9th item.
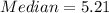
(c): Who has a better record
Statistically, the average ERA of New York Yankees is better than the average ERA of Baltimore Orioles.
Hence, New York Yankees hold the better record