Question

Coulomb's law for the magnitude of the force FFF between two particles with charges QQQ and Q′Q′Q^\prime separated by a distance ddd is

|F|=K|QQ′|d2|F|=K|QQ′|d2,
where K=14πϵ0K=14πϵ0, and ϵ0=8.854×10−12C2/(N⋅m2)ϵ0=8.854×10−12C2/(N⋅m2) is the permittivity of free space.
Consider two point charges located on the x axis: one charge, q1q1q_1 = -11.5 nCnC , is located at x1x1x_1 = -1.675 mm ; the second charge, q2q2q_2 = 40.0 nCnC , is at the origin (x=0.0000)(x=0.0000).
What is the force exerted by these two charges on a third charge q3q3q_3 = 48.0 nCnC placed between q1q1q_1 and q2q2q_2 at x3x3x_3 = -1.215 mm ?
Your answer may be positive or negative, depending on the direction of the force.
Express your answer numerically in newtons to three significant figures.

Answer 1

F_total = -65.5 N

Step-by-step explanation:

Coulomb's law is

F =
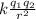`k (q_1 q_2)/(r^2)`k q1q2 / r2

In this exercise the force on the charge q3 is asked, for this we use that the force is a vector

F_total = F₁₃ + F₂₃

let's look for every force

F₁₃ =
`k (q_1 q_3)/(r_(13)^2)`

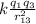
it is indicated that charge 1 is equal to q₁ = -11.5 nC = -11.5 10⁻⁹ C, located at x₁ = -1.675 mm = -1.675 10⁻³ m and charge q₃ = 48.0 nC = 48.0 10⁻⁹ C located at x₃ this position is not written in the exercise, suppose the position x₃ = -0.5 mm = 0.5 10⁻³ m

the distance is

r₁₃ =
`√((x_3 - x_1 )^2)`

r₁₃ =
`√((0.5-1.675)^2) \ 10^(-3)`

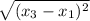
r₁₃ = 1.175 10⁻³ m

we calculate

F₁₃ =
`(9 \ 10^(9) 11.5\ 10^(-9) 48.0\ 10^(-9) )/((1.175 10^(-3))^2 )`

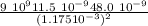
F₁₃ = 3.598 N

as the charge q₁ is negative and the charge q₃ is positive the force is attractive directed to the right

we look for F₂₃, where q₂ = 40 nC = 40.0 10⁻⁹ C located at x₂ = 0

F₂₃ =
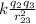
`k (q_2q_3)/(r_(23)^2)`

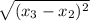
r₂₃ =
`√((x_3-x_2)^2)`

r₂₃ =
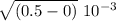`√((0.5 -0)) \ 10^(-3)`RA (-0.5 0) 2 103

r₂₃ = 0.5 10⁻³ m

F₂₃ =
`(9 \ 10^(9)\ 40\ 10^(-9) \ 48.0\ 10^(-9) x)/((0.5 \ 10^(-3))^2 )`

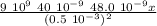
F₂₃ = 6.912 10¹ N

F₂₃ = 69.12 N

as the two charges are of the same sign, the force is repulsive, therefore it is directed to the left

the total force is

F = total = 3.598 - 69.12

F_total = -65.5 N

the negative sign indicates that the force is to the left