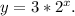Final answer:
To write an exponential function that passes through the points (0, 3) and (1, 6), we can use the general form of an exponential function and solve for the variables 'a' and 'b'. The resulting function is
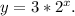
Step-by-step explanation:
To write an exponential function that passes through the points (0, 3) and (1, 6), we can start with the general form of an exponential function, which is
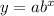 , where 'a' is the initial value and 'b' is the base.
, where 'a' is the initial value and 'b' is the base.
Using the first point (0, 3), we can substitute x = 0 and y = 3 into the function and solve for 'a':
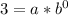
Since any number raised to the power of 0 is 1, we have:
3 = a * 1
a = 3
Now, using the second point (1, 6), we can substitute x = 1, y = 6, and 'a' = 3 into the function and solve for 'b':
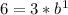
b = 6/3 = 2
Therefore, the exponential function that passes through the points (0, 3) and (1, 6) is