Question

For the given hypothesis test, determine the probability of a Type II error or the power, as specified. A hypothesis test is to be performed to determine whether the mean waiting time during peak hours for customers in a grocery store has increased from the previous mean waiting time of 8.3 minutes. Preliminary data analyses indicate that it is reasonable to apply a -test. The hypotheses are H 0: μ = 8.3 H1: >8.3 The population standard deviation is 3.8 minutes. The sample size is 50. The significance level is 0.05. Find the probability of a Type II error if in fact the mean waiting timeu, is 9.8 minutes. A. 0.125 B. 0.05 C. 0.875 D. 0.95

Answer 1

the probability of a Type II error if in fact the mean waiting time u, is 9.8 minutes is 0.1251

Option A) is the correct answer.

Step-by-step explanation:

Given the data in the question;

we know that a type 11 error occur when a null hypothesis is false and we fail to reject it.

as in it in the question;

obtained mean is 9.8 which is obviously not equal to 8.3

But still we fail to reject the null hypothesis says mean is 8.3

Hence we have to find the probability of type 11 error

given that; it is right tailed and o.5, it corresponds to 1.645

so

z is equal to 1.645

z = (x-μ)/
`(S)/(√(n) )`

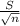
where our standard deviation s = 3.8

sample size n = 50

mean μ = 8.3

we substitute

1.645 = (x - 8.3)/
`(3.8)/(√(50) )`

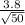
1.645 = (x - 8.3) / 0.5374

0.884023 = x - 8.3

x = 0.884023 + 8.3

x = 9.18402

so, by general rule we will fail to reject the null hypothesis when we will get the z value less than 1.645

As we reject the null hypothesis for right tailed test when the obtained test statistics is greater than the critical value

so, we will fail to reject the null hypothesis as long as we get the sample mean less than 9.18402

Now, for mean 9.8 and standard deviation 3.8 and sample size 50

Z = (9.18402 - 9.8)/
`(3.8)/(√(50) )`

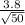
Z = -0.61598 / 0.5374

Z = - 1.1462 ≈ - 1.15

from the z-score table;

P(z<-1.15) = 0.1251

Therefore, the probability of a Type II error if in fact the mean waiting time u, is 9.8 minutes is 0.1251

Option A) is the correct answer.