Question

A veterinarian wants to know if pit bulls or golden retrievers have a higher incidence of tooth decay at the age of three. The vet surveys 120 three-year-old pit bulls and finds 30 of them have tooth decay. The vet then surveys 160 three-year-old golden retrievers and finds 32 of them have tooth decay. Number the population of pit bulls and golden retrievers by 1 and 2, respectively. Calculate a 90% confidence interval for the difference in the population proportion of pit bulls and golden retrievers that have tooth decay. Which of the following is correct?

A) [-0.0492, 0.1492]
B) [-0.0332, 0.1332]
C) [0.0199. 0.0801]
D) [0.0428, 0.0572]

Answer 1

Answer: B) [-0.0332,0.1332]

Explanation: Confidence Interval is an interval where we can be a percentage sure the true mean is.

The confidence interval for a difference in population proportion is calculated following these steps:

First, let's find population proportion for each population:

`p_(1)=(30)/(120)=0.25`

`p_(2)=(32)/(160)=0.2`

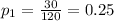
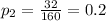
Second, calculate standard deviation for each proportion:

`\sigma_(1)=\sqrt{(0.25(0.75))/(120) } = 0.0395`

`\sigma_(2)=\sqrt{(0.2(0.8))/(160) } = 0.0316`

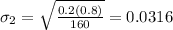
Now, we calculate standard error for difference:

`SE=\sqrt{\sigma_(1)^(2)+\sigma_(2)^(2)}`

`SE=\sqrt{0.0395^(2)+0.0316^(2)}`

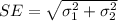
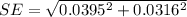
SE = 0.0505

The z-score for a 90% CI is 1.645.

Then, confidence interval is

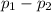`p_(1)-p_(2)` ± z-score.SE

`0.25-0.2` ±
`1.645(0.0505)`

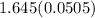
0.05 ± 0.0831

The limits of this interval are:

inferior: 0.05 - 0.0831 =
`-0.0332`

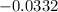
superior: 0.05 + 0.0831 = 0.1332

The 90% confidence interval for the difference in the population proportion of pit pulls and golden retrievers is
`[-0.0332,0.1332]`.