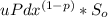Question

Adigital option is one in which the payoff depends in a discontinuous way on the asset price. The simplest example is the cash-or-nothing option, in which the payoff to the holder at maturity T is X1{ST>K} where X is some prespecified cash sum. Suppose that an asset price evolves according to the binomial model in which, at each step, the asset price moves from its current value Sn to one of Snu and Snd. As usual, if T denotes the length of each time step, d < erT < u. Find the time zero price of the above option. You may leave your answer as a sum.

Answer 1

`V_(0) = e^(-rt)` ∑
`uPdx^((1-p)) *S_(o)`

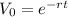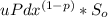
Explanation:

The Payoff to the holder at maturity T = X1{ST > K}, where X = pre-specified cash sum.

Current value of asset price = Sn after evolvement of asset price in reference to binomial model

Hence at every step value changes to SnU and Snd

where ; d < e^rΔT < u and Δ T = length of each step

u = ups

d = downs

Determine the time zero price of the above option

First we will find the price after each period

After one period :

when the price goes up, Sn + ΔT = Su

when the price goes down, Sn + ΔT = Sd

After period two

For Su

when price goes up, Sn +2ΔT = Su2

when price goes down, Sn +2ΔT = Sud

For Sd

when price goes down, Sn +2ΔT = Sd2

when price goes up, Sn +2ΔT = Sdu

To get the time zero price we will have to apply the same procedure in reverse position den get the sum pf all ups and downs which is

sum of all ups and downs =
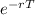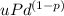
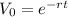`e^(-rT)`∑
`uPd^((1-p))`

`V_(0) = e^(-rt)` ∑
`uPdx^((1-p)) *S_(o)`