Question

A group of students launches a model rocket in the vertical direction. Based on tracking data, they determine that the altitude of the rocket was 89.6 ft at the end of the powered portion of the flight and that the rocket landed 16.5 s later. The descent parachute failed to deploy so that the rocket fell freely to the ground after reaching its maximum altitude. Assume that g = 32.2 ft/s2.

Determine
(a) the speed v1 of the rocket at the end of powered flight,
(b) the maximum altitude reached by the rocket.

Answer 1

`u = 260.22m/s`

`S_(max) = 1141.07ft`

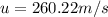
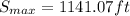
Step-by-step explanation:

Given

`S_0 = 89.6ft` --- Initial altitude

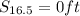`S_(16.5) = 0ft` -- Altitude after 16.5 seconds

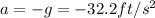`a = -g = -32.2ft/s^2` --- Acceleration (It is negative because it is an upward movement i.e. against gravity)

Solving (a): Final Speed of the rocket

To do this, we make use of:

`S = ut + (1)/(2)at^2`

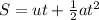
The final altitude after 16.5 seconds is represented as:

`S_(16.5) = S_0 + ut + (1)/(2)at^2`

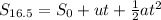
Substitute the following values:

`S_0 = 89.6ft`
`S_(16.5) = 0ft`
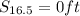
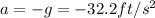`a = -g = -32.2ft/s^2` and
`t = 16.5`

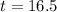
So, we have:

`0 = 89.6 + u * 16.5 - (1)/(2) * 32.2 * 16.5^2`

`0 = 89.6 + u * 16.5 - (1)/(2) * 8766.45`

`0 = 89.6 + 16.5u- 4383.225`

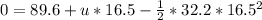
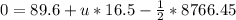
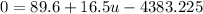
Collect Like Terms

`16.5u = -89.6 +4383.225`

`16.5u = 4293.625`

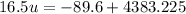
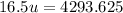
Make u the subject

`u = (4293.625)/(16.5)`

`u = 260.21969697`

`u = 260.22m/s`

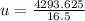
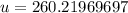
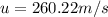
Solving (b): The maximum height attained

First, we calculate the time taken to attain the maximum height.

Using:

`v=u + at`

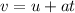
At the maximum height:

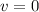`v =0` --- The final velocity

`u = 260.22m/s`

`a = -g = -32.2ft/s^2`

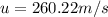
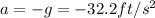
So, we have:

`0 = 260.22 - 32.2t`

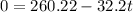
Collect Like Terms

`32.2t = 260.22`

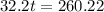
Make t the subject

`t = (260.22)/( 32.2)`

`t = 8.08s`

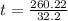
The maximum height is then calculated as:

`S_(max) = S_0 + ut + (1)/(2)at^2`

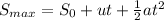
This gives:

`S_(max) = 89.6 + 260.22 * 8.08 - (1)/(2) * 32.2 * 8.08^2`

`S_(max) = 89.6 + 260.22 * 8.08 - (1)/(2) * 2102.22`

`S_(max) = 89.6 + 260.22 * 8.08 - 1051.11`

`S_(max) = 1141.0676`

`S_(max) = 1141.07ft`

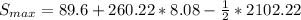
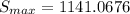
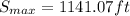
Hence, the maximum height is 1141.07ft