Question

Review Conceptual Example 8 before starting this problem. A block is attached to a horizontal spring and oscillates back and forth on a frictionless horizontal surface at a frequency of 3.96 Hz. The amplitude of the motion is 5.95 x 10-2 m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. (a) What is the amplitude and (b) the frequency of the simple harmonic motion that exists after the block splits

Answer 1

a) A' = 0.345 m, b) f = 2,800 Hz

Step-by-step explanation:

b) The angular velocity of a simple harmonic motion is

w =
`\sqrt{(k)/(m) }`

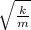
angular velocity and frequency are related

w = 2π f

we substitute

f = 1 /2π √k/m

indicates that the initial frequency value f = 3.96 Hz

in this case the mass is reduced by half

m ’= m / 2

we substitute

f = 2π
`\sqrt{(k)/(m) }`

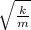
f = √1/2 (2π √k/m)

f = 1 /√2 3.96

f = 2,800 Hz

a) The amplitude of the movement is defined by the value of the initial depalzamienot before an external force that initiates the movement.

When the block is divided into two parts of equal masses as if it were exploding, for which we can use the conservation of moment

initial instant. Right before the division

p₀ = (m₁ + m₁) v

final instant. Right after the split

p_f = m₁ v '

p₀ = p_f

(2 m₁) v = m₁ v ’

v ’= 2v

At this point we can use conservation of energy for the system with only half the block.

Starting point. Where the block divides

Em₀o = K = ½ m v'²

Final point. Point of maximum elongation

Em_f = Ke = ½ k A²

how energy is conserved

Em₀ = Em_f

½ m’ v’² = ½ k A’²

we substitute the previous expressions

½ m/2 (2v)² = ½ k A’²

A’² = 2 m v² / k (1)

Let's use the conservation of energy with the initial conditions, before dividing the block

½ m v2 = ½ k A2

A² = mv² / k = 5.95 10⁻² m²

we substitute in 1

A'² = 2 A²

A ’²= 2 5.95 10⁻²

A ’²= 11.9 10⁻² m

A' = 0.345 m