Answer:
t_{out} =
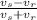 t_{in}, t_{out} =
t_{in}, t_{out} =

Step-by-step explanation:
This in a relative velocity exercise in one dimension,
let's start with the swimmer going downstream
its speed is
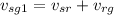
The subscripts are s for the swimmer, r for the river and g for the Earth
with the velocity constant we can use the relations of uniform motion
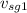 = D /
= D /
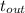
D = v_{sg1} t_{out}
now let's analyze when the swimmer turns around and returns to the starting point
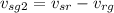
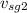 = D /
= D /
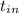
D = v_{sg 2} t_{in}
with the distance is the same we can equalize
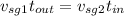
t_{out} = t_{in}
t_{out} =
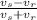 t_{in}
t_{in}
This must be the answer since the return time is known. If you want to delete this time
t_{in}= D /
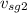
we substitute
t_{out} = \frac{v_s - v_r}{v_s+v_r} ()
t_{out} =
