Question

Four electrons and one proton are at rest, all at an approximate infiitne distance away from each other. This original arrangment of the four particles is defined as having zero electrical potential energy No work is required to bring one electron from infitinty to a location defined as the origin, while the other three particles remain at infiniuty. This is because no voltage exists near the origin until the first electron arrives. (a) Now, with the first electron remaining fixed at the origin, how much work is required to bring one of the remaining electrons from infinity to the coordinate (0 m, 2.00 m)? The other three particles remain at infinity. If this second electron was subsequently released, how fast would it be traveling once it returned to infinity? (b) Nļw, considering the two electrons fixed 2.00 m apart, how much work is required to bring the third electron from infinity to the coordinate (3.00 m, 0 m)? The other two particles remain at infinity. If this third electron was subsequently released, how fast would it be traveling once it returned to infinity? (c) Now considering the three fixed electrons at the coordinates described above. How much work is required to bring the last electron from infinity to the coordinate (3.00 m, 4.00 m)? If this forth electron was subsequently released, how fast would it be traveling once it returned to infinity? (d) Now considering the three fixed electrons at the coordinates described above. Finally, how much work is required to bring the proton from infinity to a coordinate of (1.00 m, 1.00 m)? If the proton is subsequently released and we assume that minimum separation distance between a proton and an electron is 1.00 pm, then how fast will the proton be traveling once it crashes into an electron?

Answer 1

a) W = 1.63 10⁻²⁸ J, b) W = 1.407 10⁻²⁷ J, c) W = 1.68 10⁻²⁸ J,

d) W = - 4.93 10⁻²⁸ J

Step-by-step explanation:

a) In this problem we have an electron at the origin, work is requested to carry another electron from infinity to the point x₂ = 0, y₂ = 2.00m

If we use the law of conservation of energy, work is the change in energy of the system

W = ΔU = U_∞ -U

the potential energy for point charges is

U =k
`\sum (q_i q_j)/(r_(ij) )`

in this case we only have two particles

U = k
`(q_1q_2)/(r_(12) )`

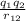
the distance is

r₁₂ =
`√((x_2-x_1)^2 + ( y_2-y_1)^2 )`

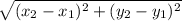
r₁₂ =
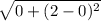`√( 0 + ( 2-0)^2)`Ra 0 + (2-0)

r₁₂ = √2= 1.4142 m

we substitute

W = k \sum \frac{q_i q_j}{r_{ij} }

let's calculate

W =
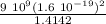`( 9 \ 10^9 (1.6 \ 10^(-19))^2 )/(1.4142)` 9 109 1.6 10-19 1.6 10-19 / 1.4142

W = 1.63 10⁻²⁸ J

b) the two electrons are fixed, what is the work to bring another electron to x₃ = 3.00 m y₃ = 0

in this case we have two fixed electrons

U = k
`( (q_1q_3)/(r_(13) ) + (q_2q_3)/(r_(23) ) )`

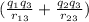
in this case all charges are electrons

q₁ = q₂ = q₃ = q

W = U = k q²
`( (1)/(r_(13) ) + (1)/(r_(23) ) )`

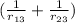
the distances are

r₁₃ =
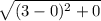`√((3-0)^2 + 0)`RA (3.00 -0) 2 + 0

r₁₃ = 3

r₂₃ =
`√( 3^2 + 2^2)`Ra (3 0) 2 + (2 0) 2

r₂₃ = √13

r₂₃ = 3.606 m

let's look for the job

W = U

let's calculate

W =
`{9 \ 10^3 ( 1.6 10^(-19))^2 }({(1)/(3) + (1)/(3.606) } )`

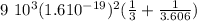
W = 1.407 10⁻²⁷ J

c) the three electrons are fixed, we bring the four electron to x₄ = 3.00m,

y₄ = 4.00 m

W = U = k
`( (q_1q_4)/(r_(14 )) + (q_2q_4)/(r_(24) ) + (q_3q_4)/(r_(34) ) )`

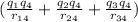
all charges are equal q₁ = q₂ = q₃ = q₄ = q

W = k q²
`((1)/(r_(14) ) + (1)/(r_(24) ) + (1)/(r_(34) ) )`

let's look for the distances

r₁₄ =
`√(3^2 +4^2)`

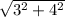
r₁₄ = 5 m

r₂₄ =
`√(3^2 + ( 4-2)^2)`

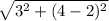
r₂₄ = √13 = 3.606 m

r₃₄ =
`√((3-3)^2 + (4-0)^2)`

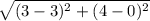
r₃₄ = 4 m

we calculate

W = 9 10⁹ (1.6 10⁻¹⁹)²
`( (1)/(5) + (1)/(3.606) + (1)/(4) )`

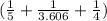
W = 1.68 10⁻²⁸ J

d) we take the proton to the location x5 = 1m y5 = 1m

W = U = k
`( (q_1q_5)/(r_(15) ) + (q_2q_5)/(r_(25) ) + (q_3q_5)/(r_(35) ) + (q_4q_5)/(r_(45) ) )`

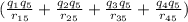
in this case the charges have the same values ​​but charge 5 is positive and the others negative, so the products of the charges give a negative value

W = - k q²
`( (1)/(r_(15) ) + (1)/(r_(25) ) + (1)/(r_(35) ) + (1)/(r_(45) ) )`

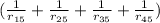
we look for distances

r₁₅ =
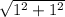`√( 1^2 +1^2)`Ra (1-0) 2 + (1-0) 2

r₁₅ = √ 2 = 1.4142 m

r₂₅ =
`√( (2-1)^2 +1^2)`

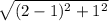
r₂₅ = √2 = 1.4142 m

r₃₅ =
`√( ( 3-1)^2 +1^2)`

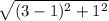
r₃₅ = √5 = 2.236 m

r₄₅ =
`√( (3-1)^2 + (4-1)^2)`

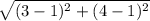
r₄₅ = √13 = 3.606 m

we calculate

W = - 9 10⁹ (1.6 10⁻¹⁹)²
`( (1)/(1.4142) +(1)/(1.4142) + (1)/(2.236) + (1)/(3.606) )`

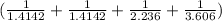
W = - 4.93 10⁻²⁸ J