1 Answer

Allon · Answer 1 · 2022-12-13T10:44:33+0000

Answer:

a) 0.5664 = 56.64% probability that the urn selected was the first one.

b) 0.4336 = 43.36% probability that the urn selected was the second one

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probability of event B happening, given that A happened.

$P(A \cap B)$ is the probability of both A and B happening.

P(A) is the probability of A happening.

If both balls are white, what are the following probabilities?

This means that event A is both balls being white.

Probability of both balls being white:

0.8 probability of 4/10 = 0.4 squared(first urn, which each time the ball is drawn will have 4 white balls and 6 red)

1 - 0.8 = 0.2 probability of 7/10 = 0.07 squared(second urn). So

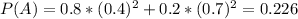
P(A) = 0.8*(0.4)^2 + 0.2*(0.7)^2 = 0.226

a. the probability that the urn selected was the first one

Event B: First urn selected.

The intersection of events A and B is given by both balls being white and selected from the first urn, which has the following probability:

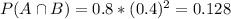
$P(A \cap B) = 0.8*(0.4)^2 = 0.128$

The desired probability is:

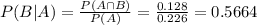
$P(B|A) = (P(A \cap B))/(P(A)) = (0.128)/(0.226) = 0.5664$

0.5664 = 56.64% probability that the urn selected was the first one

b. the probability that the urn selected was the second one

The intersection of events A and B is given by both balls being white and selected from the second urn, which has the following probability:

$P(A \cap B) = 0.2*(0.7)^2 = 0.098$

The desired probability is:

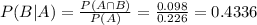
$P(B|A) = (P(A \cap B))/(P(A)) = (0.098)/(0.226) = 0.4336$

0.4336 = 43.36% probability that the urn selected was the second one

Please log in or register to add a comment.