Question

An experimental psychologist plans a study in which a crucial step is offering participants a food reward. It is important that the three food rewards be equal in appeal. Thus, a prestudy was designed in which participants were asked which of the rewards they preferred. Of the 60 participants, 16 preferred cupcakes, 26 preferred candy bars, and 18 favored dried apricots. Do these scores suggest that the different foods are differentially preferred by people in general? (Use the .05 significance level.)

You must use all five steps in hypothesis testing:
Restate the question as a research hypothesis and a null hypothesis about the populations.
Determine the characteristics of the comparison distribution.
Determine the cutoff sample score on the comparison distribution at which the null hypothesis should be rejected.
Determine your sample’s score on the comparison distribution.
Decide whether to reject the null hypothesis.

Answer 1

Explanation:

From the information given:

`\mathbf{H_o: there \ is \ no \ significanr \ difference \ between \ observed \ and \ expected \ value }`

`\mathbf{H_a: there \ is \ significanr \ difference \ between \ observed \ and \ expected \ value }`

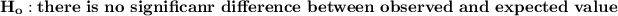
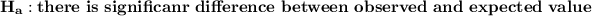
The characteristic of the comparison is a uniform distribution.

Since there are three categories from the data, then: the data obeys a U(0,3) distribution. However, supposed it happened that different food had the same appeal, thus, there will be uniform distribution in the preference score.

`Degree \ of \ freedom \ df = n - 1 \\ \\ df = 3 - 1 = 2`

At 0.05;

Thus, at 0.05 and df of 2, the cutoff sample score at which
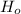`H_o` will be reject is the critical value
`\mathbf{X_(0.05,2)^2 \ which \ is \ = 5.991}`

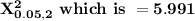
Prefered Observed Expected Expected (O - E) (O - E)²/ E

frequency frequency proportions

Cup cakes 16 20 0.333 -4.00 0.800

Candy bars 26 20 0.333 6.00 1.800

Dried apricots 18 20 0.333 -2.00 0.200

Total 60 20 1 -2.00 2.800

Thus the sample score is
`\mathbf{X^2_(observed) = 2.800}`

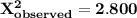
Decision rule: To reject the null hypothesis if the observed test statistic is higher than the critical value.

Conclusion: We fail to reject the null hypothesis and conclude that different foods have the same appeal to different people.