Question

You have 17 liters of gas at STP. If the temperature rises to 94C and while the volume decreases to 12 liters, what will the new pressure be?

Answer 1

`P_2=1.90atm`

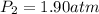
Step-by-step explanation:

Hello!

In this case, according to the ideal gas equation ratio for two states:

`(P_1V_1)/(P_2V_2) =(n_1RT_1)/(n_2RT_2)`

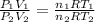
Whereas both n and R are cancelled out as they don't change, we obtain:

`(P_1V_1)/(P_2V_2) =(T_1)/(T_2)`

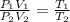
Thus, by solving for the final pressure, we obtain:

`(P_2V_2)/(P_1V_1) =(T_2)/(T_1)\\\\P_2=(T_2P_1V_1)/(V_2T_1)`

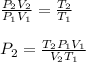
Now, since initial conditions are 1.00 atm, 273.15 K and 17 L and final temperature and volume are 94 + 273 = 367 K and 12 L respectively, the resulting pressure turns out to be:

`P_2=(367K*1.00atm*17L)/(12L*273.15K)\\\\P_2=1.90atm`

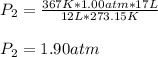
Best regards!