To ensure differentiability of f(x) at x=-4 , set the left- and right-hand derivatives equal: a = 8b + 5 . The quadratic equation resulting from continuity yields b = 2 and a = 17 .
To determine the values of `a` and `b` which would result in the function `f(x)` being differentiable at `x=-4`, we need to make sure that the left- and right-hand derivatives of `f(x)` at `x=-4` are equal.
Left-hand derivative:
f'(-4)=a
Right-hand derivative:
f'(-4)=2b(-4)+5=8b+5
Setting these two derivatives equal, we get:
a=8b+5
This is one equation with two unknowns, so we need another equation in order to solve for `a` and `b`.
We can use the fact that `f(x)` is continuous at `x=-4`. This means that the two expressions for `f(x)` at `x=-4` must be equal.

Substituting `a=8b+5` into this equation, we get:
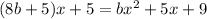
Simplifying both sides of this equation, we get:
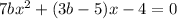
This is a quadratic equation in `x`. In order for `f(x)` to be differentiable at `x=-4`, the roots of this quadratic equation must be equal. This means that the discriminant of the quadratic equation must be zero.
 -4*7b*(-4)=0
-4*7b*(-4)=0
Solving for `b`, we get:
b=2
Substituting `b=2` into the equation `a=8b+5`, we get:
a=17`
Therefore, the values of `a` and `b` which would result in the function `f(x)` being differentiable at `x=-4` are a=17` and b=2`.