Question

14. Velocity of ball is 31 A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km b Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h What is the ad magnitude of average velocity, and the average speed of the man over the interval of time i) 0 to 30 min. (i) 0 to 50 min. (iii) 0 to 40 min? ​

Answer 1

The man's average velocity is zero, and average speed varies, peaking at 3.75 km/hr in 0 to 40 minutes and lowest at 2.5 km/hr in 0 to 30 minutes.

The man's journey can be divided into two segments: the outbound walk from home to the market and the return walk from the market to home. The distance covered in each segment is the same, as he returns to his starting point.

(i) **0 to 30 minutes:**

- In the first 30 minutes, the man covers half of the total distance (1.25 km) towards the market.

- Average velocity is the displacement over time. Since he returns to his starting point, the displacement is zero.

- Average speed is the total distance covered over time. So, average speed is
`\(\frac{1.25 \, \text{km}}{0.5 \, \text{hr}} = 2.5 \, \text{km/hr}\).`

(ii) **0 to 50 minutes:**

- In the first 50 minutes, he covers the entire distance to the market (2.5 km).

- Average velocity is the displacement over time, which is zero since he returns home.

- Average speed is
`\(\frac{2.5 \, \text{km}}{0.8333 \, \text{hr}} \approx 3 \, \text{km/hr}\).`

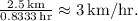
(iii) **0 to 40 minutes:**

- In the first 40 minutes, he covers more than half of the total distance but doesn't reach the market.

- Average velocity is still zero due to returning home.

- Average speed is
`\(\frac{\text{distance covered}}{\text{time}} = \frac{\text{distance to market}}{0.667 \, \text{hr}} \approx 3.75 \, \text{km/hr}\).`

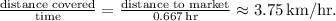
The man's average velocity is zero as he returns home in all intervals. The average speed varies, being highest in the 0 to 40 minutes interval and lowest in the 0 to 30 minutes interval.