Question

In Exercises 17-20, tell whether the orthocenter of the triangle with

triangle. Then find the coordinates of the orthocenter. L(0, 5), M(3, 1), N(8, 1)

Answer 1

(0,-5) is the coordinates of the orthocenter, of the triangle ΔLMN with the vertices L(0,5), M(3, 1) and N(8, 1).

Let H(x, y) be the orthocenter of ΔLMN.

Let,
`L_(1)`,
`L_(2)` be the perpendiculars of sides LN, NM respectively.

From the graph we infer that the coordinate of the orthocenter lies outside the ΔLMN. Since L₁ is perpendicular to LN and L₂ is perpendicular to NM

Slope of L₁
`x` Slope of LN= -1 …… (1)

Slope of L₂
`x` Slope of NZ= -1 …… (2)

We know that, if m is the slope of the line formed by joining the points (,
`X_(1) }`,
`Y_(1) }`) and (
`{X_(2),{Y_(2)`) then,

`m=(Y_(2)-Y_(1) )/(X_(2)-X_(1) )` …… (3)

If m is a slope of a line and (
`X_(1) }`,
`Y_(1) }`) are the points on the line, then the equation of the line

`m= (y-Y_(1) )/(x-X_(1) )` …… (4)

Substituting the points of the line LN in equation (3)

Slope of LN =
`(5-1)/(0-8)`

=
`(-4)/(8)`

=
`-(1)/(2)`

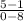
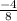
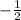
Similarly, substitute the points of the line LM in equation (3)

Slope of LM =
`(1-5)/(3-0)`

=
`-(4)/(3)`

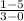
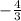
Substituting the slope of LN in equation (1), we get Slope of L₁=2

By substituting the point M(3,1) and Slope of L₁ in equation (4), we get

`2=(y-1)/(x-3)`

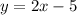`y=2x-5` …… (5)

Substituting the slope of LM in equation (2), we get Slope of L₂=
`(3)/(4)`

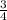
By substituting the point N(8,1) and Slope of L₂ in equation (4), we get

`(y-1)/(x-8) = (3)/(4)`

`3x-4y=20` …… (6)

From equation (5)

`y=2x-5`

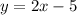
Substituting
`x` in equation (6), we get

`3x-4(2x-5) = 20`

`3x-8x+20=20`

`-5x=0`

`x=0`

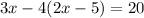
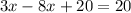
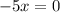
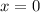
Substituting the value of
`x` in equation (6), we get

`3(0) - 4y = 20`

`- 4y = 20`

`y = -5`

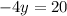
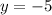
So, H(0, -5) is the orthocenter of the ΔLMN.