Question

Two glasses have same level of water in them. The amount of water in the first glass increased by 1% of the current amount and , then by 2% and then by 3% and so on until the final increase by 27%. The amount of water in the second glass was first increased by 27% and then by 26% and so on until the final increase by 1%. Given that the glasses cannot be overfilled , which glass has greater amount of water in it?

Answer 1

Both glasses have the same final amount of water since the cumulative increase in the first glass (1% to 27%) equals the cumulative decrease in the second glass (27% to 1%).

Let's break down the calculations step by step:

1. First Glass (Increasing):

- Let the initial amount of water be 100 units.

- The increase for each step is 1%, 2%, 3%, ..., up to 27%.

- The total increase is the sum of the first 27 natural numbers:
`\((27 * 28)/(2) = 378\).`

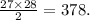
2. Second Glass (Decreasing):

- Assume the initial amount of water is also 100 units.

- The decrease for each step is 27%, 26%, 25%, ..., down to 1%.

- The total decrease is also the sum of the first 27 natural numbers:
`\((27 * 28)/(2) = 378\).`

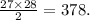
3. Comparison:

- Both glasses experience a cumulative change of 378 units, whether through increase or decrease.

- Therefore, the final amount of water in both glasses is the same, and neither glass is overfilled.

In conclusion, both glasses have an equal amount of water, maintaining the initial water level due to the symmetry of the percentage changes.