Question

Find the equation of the line tangent to the graph of x(t)=t²+1 and y(t)=


`√(1 + t)`at point t=3​

Answer 1

The equation of the straight line

x - 24y + 38 =0

Explanation:

Step(i):-

Given that x(t) = t²+1 ..(i)

and y(t) = √1+t ..(ii)

Differentiating equation(i) with respective to 't'

`(dx)/(dt) = 2t`

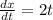
Differentiating equation(ii) with respective to 't'

`(dy)/(dt) = (1)/(2√(1+t) )`

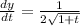
Step(ii):-

The slope of the tangent

`m = (dy)/(dx) = ((dy)/(dt) )/((dx)/(dt) ) = ((1)/(2√(1+t) ) )/(2t)`

`m =( (dy)/(dx) )_(t=3) = (1)/(4(3)√(1+3) )`

`m = (1)/(24)`

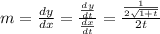
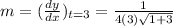
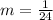
Step(iii):-

Point x = t²+1 = 3²+1 = 10

y = √1+t =√1+3 = √4 =2

The point on the tangent line is ( 10 ,2)

The equation of the straight line

`y - y_(1) = m( x-x_(1) )`

`y - 2 = (1)/(24) ( x-10 )`

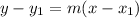
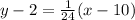
24 (y-2) = x-10

24y - 48 = x-10

x - 24 y -10 +48 =0

x - 24y + 38 =0

Final answer:-

The equation of the straight line

x - 24y + 38 =0