Question

12) please only answer if you can help!!

Answer 1

The ellipse equation is (x^2/81) + (y^2/36) = 1. This means center at origin, major radius 9, and minor radius 6.

The ellipse equation is (x^2 / 81) + (y^2 / 36) = 1. This means the center is at the origin, major radius is 9, and minor radius is 6.

The ellipse graphed in the image has a horizontal major axis, so its equation will be in the form:

`(x - h)^2 / a^2 + (y - k)^2 / b^2`= 1

where (h, k) is the center of the ellipse, a is the length of the major radius, and b is the length of the minor radius.

From the graph, we can see that the center of the ellipse is at the origin, (0, 0). The major radius is the distance from the center to the horizontal vertices, which is 9 units. The minor radius is the distance from the center to the vertical vertices, which is 6 units.

Therefore, the equation of the ellipse in standard form is:

`x^2 / 9^2 + y^2 / 6^2` = 1

more simply:

`x^2 / 81 + y^2 / 36`= 1

This equation can be rewritten in a more compact form by introducing a new constant, c, which represents the distance between a focus of the ellipse and the center:

`(x - h)^2 / a^2 + (y - k)^2 / b^2` = 1

`(x - 0)^2 / 9^2 + (y - 0)^2 / 6^2`= 1

`x^2 / 81 + y^2 / 36` = 1

`(x^2 + 2y^2)` / 81 = 1

`c^2` =
`a^2` -
`b^2`

`c^2` =
`9^2` -
`6^2`

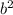
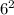
`c^2` = 27

c = sqrt(27) =
`3√(3)`

Therefore, the equation of the ellipse in terms of c is:

`(x^2 + 2y^2)`/ 81 =
`c^2`/ 81

`x^2 + 2y^2`=
`c^2`

`x^2 + 2y^2 = (3√(3))^2`

`x^2 + 2y^2 = 27`

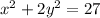
This is the equation of the ellipse graphed in the image, in standard form.

The equation for the ellipse graphed above is:

`x^2 / 81 + y^2 / 36` = 1

To find the equation of the ellipse in terms of c, the distance between a focus of the ellipse and the center, we can use the following formula:

`c^2 = a^2 - b^2`

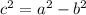
Substituting in the values for a and b, we get:

`c^2 = 9^2 - 6^2 = 27`

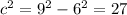
Taking the square root of both sides, we get c = 3sqrt(3).

Therefore, the equation of the ellipse in terms of c is:

`(x^2 + 2y^2) / 81 = (3sqrt(3))^2 / 81`

`x^2 + 2y^2 = 27`

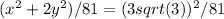
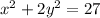
This is the equation of the ellipse graphed above, in both standard form and in terms of c.