Question

The height of a woman ages 20-29 is normally distributed, with a mean of 63.8 inches. [SD] O=2.8

Answer 1

1. It is more likely to select a sample of 16 women with a mean height less than 66.1 inches.

i. The probability of randomly selecting one woman with a height less than 66.1 inches is approximately 0.7932.

iii. The probability of selecting a sample of 16 women with a mean height less than 66.1 inches is higher, approximately 0.9994, due to the central limit theorem and the reduction in variability when considering a sample mean.

iii. The correct option is option A) It is more likely to select a sample of 16 women with a mean height less than 66.1 inches because the sample of 16 has a higher probability.

1. To answer this question, we can use the central limit theorem (CLT). The central limit theorem states that for a sufficiently large sample size, the distribution of the sample mean will be approximately normally distributed, regardless of the distribution of the population.

i. Probability for One Woman with Height Less than 66.1 inches:

• Given a normal distribution with a mean (μ) of 63.8 inches and a standard deviation (σ) of 2.8 inches, we want to find the probability that a randomly selected woman has a height less than 66.1 inches.
• Using the z-score formula:
  `\(z = ((X - \mu))/(\sigma)\)`, where
  `\(X\)` is the value,
  `\(\mu\)` is the mean, and
  `\(\sigma\)` is the standard deviation.
• For
  `\(X = 66.1\), \(z = ((66.1 - 63.8))/(2.8) \approx 0.821\)`.
• Looking up the z-score in the standard normal distribution table, we find the probability. The probability for a single woman is P(Z < 0.821), which is approximately 0.7932.

ii. Probability for Sample of 16 Women with Mean Height Less than 66.1 inches:

• Using the central limit theorem, the distribution of the sample mean will have the same mean (63.8 inches) but a standard deviation (standard error) of
  `\((\sigma)/(√(n))\)`, where
  `\(n\)` is the sample size.
• For
  `\(n = 16\)`, the standard error is
  `\((2.8)/(√(16)) = 0.7\)`.
• We calculate the z-score for the sample mean using the formula
  `\(z = \frac{(X - \mu)}{\text{standard error}}\).`
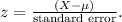
• For
  `\(X = 66.1\), \(z = ((66.1 - 63.8))/(0.7) \approx 3.29\).`
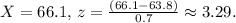
• Looking up the z-score in the standard normal distribution table, we find the probability. The probability for a sample mean is P(Z < 3.29), which is approximately 0.9994.

iii. Therefore, the correct option is option A) It is more likely to select a sample of 16 women with a mean height less than 66.1 inches because the sample of 16 has a higher probability.