The correct answer is C)
![\boxed{(3-4i)/(2)}]](https://img.qammunity.org/2024/formulas/mathematics/college/19nf8byulrozg20z6p13puaec01sase8et.png) .
.
To solve the equation, we can use the following steps:
Multiply both sides of the equation by the complex conjugate of the denominator.
![[(1+7i)/(-2+2i)]](https://img.qammunity.org/2024/formulas/mathematics/college/b9gmgcimdv2t9hawgc2zso61jqfq1wvdam.png) .
.
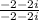
=
![((1+7i)(-2-2i))/((-2+2i)(-2-2i))]](https://img.qammunity.org/2024/formulas/mathematics/college/xci9mdueczxjfg2ux7lh4ht20vsfl5vlg5.png)
Expand the product in the numerator.

=
![[\frac{-2-2i - 14i - 14 i^2} {-4+4+4 i^2}]](https://img.qammunity.org/2024/formulas/mathematics/college/mlpriyz28ilrvs6a4d8eobw7jc1swor1kb.png)
Simplify the numerator and denominator.
![[(-2-2i - 14i + 14)/(-4+4+4 i^2)]](https://img.qammunity.org/2024/formulas/mathematics/college/mp01x5djqbhcteaf24ccz58qd66yvbmyuw.png)
=
![[(12-16i)/(-4+4 i^2)]](https://img.qammunity.org/2024/formulas/mathematics/college/tnr6bcxvippteot4tanm8ymjk3cldyx142.png)
Note that
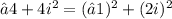
=
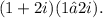
Dividing both sides by (1+2i)(1−2i), we get the solution.
![[(12-16i)/(-4+4 i^2)]](https://img.qammunity.org/2024/formulas/mathematics/college/tnr6bcxvippteot4tanm8ymjk3cldyx142.png)
=
![\boxed{(3-4i)/(2)}]](https://img.qammunity.org/2024/formulas/mathematics/college/19nf8byulrozg20z6p13puaec01sase8et.png)