Question

Triangle D E F is shown with point P at the center. Lines are drawn from each point of the triangle to point P. Line segments are drawn from point P to the sides of the triangle to form right angles and line segments P H, P J, and P G. The length of F J is 3 x minus 1, the length of J E is x + 3, the length of H E is 4 y minus 3, and the length of H D is 9.

Given that point P is equidistant from the vertices of ΔDEF, what is EF?



EF = 10

Answer 1

In triangle DEF with centroid P, lengths FJ, JE, HE, and HD are given. Solving equations based on the centroid properties yields x = 2, y = 5/4. The equidistant point P results in EF equal to 10.

Since point P is equidistant from the vertices of triangle DEF, it lies at the centroid. In a centroid, each median divides the opposite side into two segments, where the length of the segment closer to the vertex is twice the length of the segment closer to the midpoint.

Let's denote:

- FJ = 3x - 1

- JE = x + 3

- HE = 4y - 3

- HD = 9

For a centroid, the relationship is given by:

`\[ FJ = 2 \cdot JP \]`

`\[ JE = 2 \cdot JP \]`

`\[ HE = 2 \cdot JP \]`

From this, we can set up equations:

`\[ 3x - 1 = 2 \cdot JP \]`

`\[ x + 3 = 2 \cdot JP \]`

`\[ 4y - 3 = 2 \cdot JP \]`

Now, we can solve for JP in each equation:

`\[ JP = (3x - 1)/(2) \]`

`\[ JP = (x + 3)/(2) \]`

`\[ JP = (4y - 3)/(2) \]`

Since JP is equidistant from the vertices, we can set these expressions equal to each other:

`\[ (3x - 1)/(2) = (x + 3)/(2) = (4y - 3)/(2) \]`

Now, solve for x and y:

1. Solve
`\( (3x - 1)/(2) = (x + 3)/(2) \):`

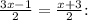
3x - 1 = x + 3

2x = 4

x = 2

2. Solve
`\( (4y - 3)/(2) = (x + 3)/(2) \) (substitute x = 2):`

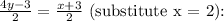
4y - 3 = 2 + 3

4y = 5

`\[ y = (5)/(4) \]`

Now, we know x = 2 and
`\( y = (5)/(4) \).`

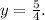
Finally, find EF:

EF = JE + JF

EF = (x + 3) + (3x - 1)

`EF = (2 + 3) + (3 \cdot 2 - 1) \]`

EF = 5 + (6 - 1)

EF = 5 + 5

EF = 10

Therefore, EF is 10.