Question

Find an equation of the tangent line to the curve at the point corresponding to the given value of the parameter. x = t cos(t), y = t sin(t); t =

Answer 1

`y = (-\pi )/(1+\pi ) . x + \pi`

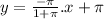
To find the equation of the tangent line to the curve x=tcos(t) and y=tsin(t) at the point corresponding to t=π, we'll follow the steps

`(dx)/(dt) = cos(t) - tsin(t)`

`(dy)/(dt) = sin(t) - tcos(t)`

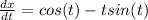
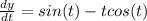
at
`t = \pi`,

`m = (sin (\pi ) + \pi cos (\pi ))/(cos(\pi) - \pi sin (\pi ) )`

`m = (-\pi )/(1+\pi )`

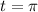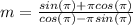
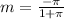
Now, we need to find the point on the curve at
`t = \pi`

`x_(0) = \pi cos (\pi ) = -\pi`

`y_(0) = \pi sin (\pi ) = 0`

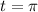
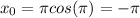
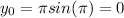
Plug in these values into the point-slope form:

`y-0= (-\pi )/(1+\pi ) . (x + \pi)`

`y= (-\pi )/(1+\pi ) . (x + \pi)`

That's the equation of the tangent line to the curve at the point corresponding to
`t = \pi`

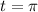
Question
Find an Equation Given the Parameter: