Question

Complete the proof.

Question 7 options:

Blank 1 is...


Blank 2 is...


Blank 3 is...

1.
Corresponding Angles Postulate

2.
Alternate Interior Angles Theorem

3.
Angle Addition Postulate

4.
Linear Pair Postulate

5.
Substitution Property

Answer 1

1. Given:

2. Alternate Interior Angles:

3. Alternate Interior Angles:

4. Angle Addition Postulate:

5. Linear Pair Postulate:

6. Substitution Property:

7. Substitution Property:

1. Given:
`\(\overleftrightarrow{CD} || \overline{AB}\)`

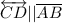
- Reason: Given information.

2. Alternate Interior Angles:

- Statement:
`\(m\angle2 = m\angle4\)`

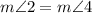
- Reason: Alternate interior angles formed by parallel lines are equal.

3. Alternate Interior Angles:

- Statement:
`\(m\angle3 = m\angle5\)`

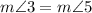
- Reason: Similarly, alternate interior angles are equal.

4. Angle Addition Postulate:

- Statement:
`\(m\angle4 + m\angle1 = m\angle DCB\)`

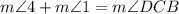
- Reason: The sum of angles on the same side of a line is equal to the angle formed by that line.

5. Linear Pair Postulate:

- Statement:
`\(m\angle DCB + m\angle5 = 180^\circ\)`

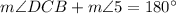
- Reason: The angles in a linear pair (adjacent and supplementary) add up to
`\(180^\circ\).`

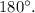
6. Substitution Property:

- Statement:
`\(m\angle4 + m\angle1 + m\angle5 = 180^\circ\)`

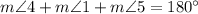
- Reason: Substituting the expression for \(m\angle DCB\) from statement 4 into statement 5.

7. Substitution Property:

- Statement:
`\(m\angle2 + m\angle1 + m\angle3 = 180^\circ\)`

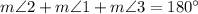
- Reason: Substituting the expressions for
`\(m\angle4\) and \(m\angle5\)` from statements 2 and 3 into statement 6.

Conclusion: The right triangle nature of the triangle, evident from the presence of a 90-degree angle. The equality of alternate interior angles, the angle addition postulate, and the linear pair postulate collectively affirm the validity of the relationships in the diagram.