Question

Isosceles triangle ABC has vertices A(3,11) and B(3,1) as the base angles. If the perimeter of triangle ABC is 56, what is a possible x-coordinate for point C? Enter your answer as a decimal rounded to the nearest hundredth if not an integer.

Your Answer:

Answer 1

With a base of 10 units and a total perimeter of 56, the isosceles triangle ABC with vertices A (3, 11) and B (3, 1) has a possible x-coordinate of 14.00 for point C.

To find a possible x-coordinate for point C:

Calculate the base length: The base length of the triangle is the difference between the y-coordinates of points A and B: 11 - 1 = 10 units.

Calculate remaining side length: The perimeter is 56 units, and the base is 10 units, so the remaining two sides must have a combined length of 56 - 10 = 46 units.

Use Pythagorean theorem: Consider the right triangle formed by the base and one of the remaining sides. Let x be the x-coordinate of point C. We can set up a Pythagorean equation:

`(x - 3)^2 + 10^2 = (46/2)^2`

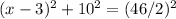
Solve for x: Simplify the equation and solve for x:

`x^2` - 6x + 9 + 100 =
`23^2`

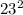
`x^2` - 6x - 124 = 0

(x - 14)(x + 9) = 0

Check for valid solutions: Only the positive solution is valid for x: x = 14.

Therefore, a possible x-coordinate for point C is 14.00.