Answer:
1) The multiplicative inverse of
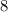 is
is
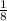 .
.
2) The multiplicative inverse of
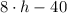 is
is
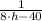 .
.
Explanation:
Mathematically, let
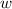 and
and
 real numbers.
real numbers.
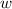 is the multiplicative inverse if and only if
is the multiplicative inverse if and only if
 . Now we proceed to determine the multiplicative inverse of each number:
. Now we proceed to determine the multiplicative inverse of each number:
1)
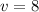
(i)
 Definition of multiplicative inverse
Definition of multiplicative inverse
(ii)
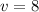 Given
Given
(iii)
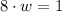 (ii) in (i)
(ii) in (i)
(iv)
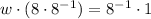 Compatibility with multiplication/Associative and commutative properties
Compatibility with multiplication/Associative and commutative properties
(v)
 Existence of multiplicative inverse/Modulative property
Existence of multiplicative inverse/Modulative property
(vi)
 Definition of division/Result
Definition of division/Result
The multiplicative inverse of
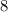 is
is
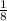 .
.
2)
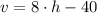
(i)
 Definition of multiplicative inverse
Definition of multiplicative inverse
(ii)
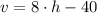 Given
Given
(iii)
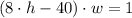 (ii) in (i)
(ii) in (i)
(iv)
![w\cdot [(8\cdot h - 40)\cdot (8\cdot h-40)^(-1)] = (8\cdot h - 40)^(-1)\cdot 1](https://img.qammunity.org/2022/formulas/mathematics/high-school/avk8jnkjh0rq9s3sk5yiqipj2ckwcyac2t.png) Compatibility with multiplication/Associative and commutative properties
Compatibility with multiplication/Associative and commutative properties
(v)
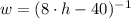 Existence of multiplicative inverse/Modulative property
Existence of multiplicative inverse/Modulative property
(vi)
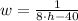 Definition of division/Result
Definition of division/Result
The multiplicative inverse of
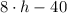 is
is
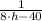 .
.