Answer:
To solve the triangle using the given information:
Given:
Side a = 10
Side b = 12
Side c = 17
We're asked to find angle A and side b.
We'll use the Law of Cosines to find angle A first:
![\[a^2 = b^2 + c^2 - 2bc \cdot \cos(A)\]](https://img.qammunity.org/2024/formulas/mathematics/college/6x4ta74rns4lt8bt7nigu804ptmsf17e9g.png)
Substitute the given values:
![\[10^2 = 12^2 + 17^2 - 2 * 12 * 17 \cdot \cos(A)\]\[100 = 144 + 289 - 408 \cdot \cos(A)\]\[100 = 433 - 408 \cdot \cos(A)\]](https://img.qammunity.org/2024/formulas/mathematics/college/v81zkomkjw95r7yppadxp5gqe489pov1fi.png)
Solving for \(\cos(A)\):
![\[-333 = -408 \cdot \cos(A)\]\[\cos(A) = (-333)/(-408)\]\[\cos(A) \approx 0.81618\]](https://img.qammunity.org/2024/formulas/mathematics/college/lr8zqtoykhuur00ywsae40oackaf31ape1.png)
Now, to find angle A, take the arccosine of 0.81618:
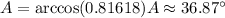
Now that we have angle A, let's use the Law of Sines to find angle B:
![\[(\sin(A))/(a) = (\sin(B))/(b)\]\[(\sin(36.87^\circ))/(10) = (\sin(B))/(12)\]](https://img.qammunity.org/2024/formulas/mathematics/college/7qb8t6jkaj33oypcl2qwrkeyo1fvhbxf42.png)
Solving for
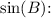
![\[\sin(B) = (12 * \sin(36.87^\circ))/(10)\]\[\sin(B) \approx 0.7017\]](https://img.qammunity.org/2024/formulas/mathematics/college/kgqqaa712udd2g1yb2v263l8pysguo0x8w.png)
Now, find angle B:
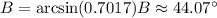
Therefore, in the triangle:
Angle A ≈ 36.87°
Angle B ≈ 44.07°
Explanation: