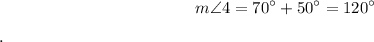
The Exterior Angle Theorem is a useful theorem in geometry, and it can be used to solve a variety of problems.
Proof of the Exterior Angle Theorem
Given:
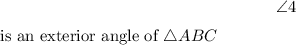
Prove:

Proof:
1.
 .
.
2.
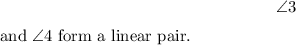 (Definition of an exterior angle)
(Definition of an exterior angle)
3.
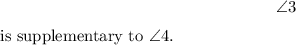 (Supplementary angles theorem)
(Supplementary angles theorem)
4.
 . (Definition of supplementary angles)
. (Definition of supplementary angles)
5.
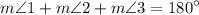 . (Triangle Sum Theorem)
. (Triangle Sum Theorem)
6.
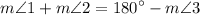 . (Subtracting
. (Subtracting
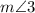 from both sides of equation 5)
from both sides of equation 5)
7.
 . (Substituting equation 4 into equation 6)
. (Substituting equation 4 into equation 6)
Therefore, the exterior angle of a triangle is equal to the sum of the two remote interior angles.
In the diagram below,
 is an exterior angle of
is an exterior angle of

[Image of a triangle ABC with an exterior angle 4]
Using the Exterior Angle Theorem, we can prove that

Proof:
1.
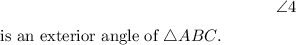
2.
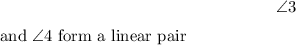
3.
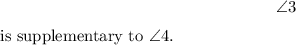
4.

5.
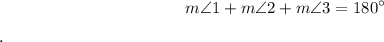
6.
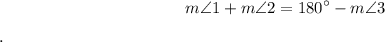
7.
