Question

The ratio of the masses and radii of two planets are 2:3 and 8:27. The ratio of respective escape speeds from their surfaces is:

a. 2:3
b. 4:9
c. 8:27
d. 16:81

Answer 1

The ratio of the masses and radii of two planets are 2:3 and 8:27. The ratio of respective escape speeds from their surfaces is 4:9

The escape speed from the surface of a planet is given by the formula:

`\[v_{\text{escape}} = \sqrt{(2GM)/(R)}\]`

where:

`\(v_{\text{escape}}\)` is the escape speed,

`\(G\)` is the gravitational constant,

`\(M\)` is the mass of the planet, and

`\(R\)` is the radius of the planet.

Let's consider two planets, planet 1 and planet 2, with masses
`\(M_1\)` and
`\(M_2\)` and radii
`\(R_1\)` and
`\(R_2\)`, respectively. The given ratios are:

`\[(M_1)/(M_2) = (2)/(3)\]`

`\[(R_1)/(R_2) = (8)/(27)\]`

Now, let's find the ratio of their escape speeds,
`\(v_{\text{escape1}}\) and \(v_{\text{escape2}}\):`

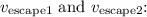
`\[\frac{v_{\text{escape1}}}{v_{\text{escape2}}} = \sqrt{((2G M_1)/(R_1))/((2G M_2)/(R_2))} = \sqrt{(M_1 R_2)/(M_2 R_1)}\]`

Substitute the given ratios:

`\[\frac{v_{\text{escape1}}}{v_{\text{escape2}}} = \sqrt{((2G \cdot (2)/(3) M_2)/((8)/(27) R_1))/((2G M_2)/(R_2))} = \sqrt{((2)/(3) \cdot (27)/(8) \cdot R_2)/(R_1)} = \sqrt{(9)/(4) \cdot (R_2)/(R_1)}\]`

Simplify:

`\[\frac{v_{\text{escape1}}}{v_{\text{escape2}}} = (3)/(2) \cdot \sqrt{(R_2)/(R_1)}\]`

Now, substitute the given ratio
`\((R_1)/(R_2) = (8)/(27)\):`

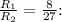
`\[\frac{v_{\text{escape1}}}{v_{\text{escape2}}} = (3)/(2) \cdot \sqrt{(1)/((8)/(27))} = (3)/(2) \cdot \sqrt{(27)/(8)} = (3)/(2) \cdot (3)/(2) = (9)/(4)\]`

So, the correct answer is:

b. 4:9

Answer 2

The ratio of the respective escape speeds from the surfaces of the two planets is 2:3. Therefore, the correct option is a. 2:3.

Step-by-step explanation:

To find the ratio of the respective escape speeds from the surfaces of the two planets, we can use the equation:

V1/V2 = √(M2/M1)

where V1 is the escape speed from the surface of the first planet, V2 is the escape speed from the surface of the second planet, M1 is the mass of the first planet, and M2 is the mass of the second planet.

Using the given ratios of masses, we have:

• M2/M1 = (2/3)^2 = 4/9

Substituting this into the equation, we find:

• V1/V2 = √(4/9) = 2/3

Therefore, the ratio of the respective escape speeds from the surfaces of the two planets is 2:3 (option a).