Answer:
16984
Explanation:
Given
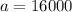 ---- Initial
---- Initial
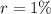 --- rate
--- rate
Required
Determine the population after 6 years
To do this, we make use of the following exponential function
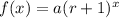
Substitute values for a and r

Express 1% and decimal
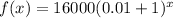
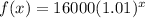
The population after 6 years is:
Substitute 6 for years
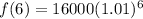
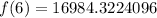
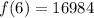 -- approximated
-- approximated