Question

Apply the Pythagorean Theorem to find the length between the two points. Round your answer to the nearest hundredth, if necessary.

5.57
41
6:40 (correct)
9
please do step by step answer as to why 6:40 is correct.

Answer 1

d≈6.40

The first two values (2,4) represent the coordinates of one point, and the last two values (-2,-1) represent the coordinates of another point, we can proceed with the Pythagorean Theorem.

Let's denote the points as follows:

Point 1: (x₁, y₁) = (2,4)

Point 2: (x₂, y₂) = (-2,-1)

The formula for the distance (d) between two points (x₁, y₁) and (x₂, y₂) is given by the Pythagorean Theorem:

`d = \sqrt{(x_(2) - x_(1) )^(2) +(y_(2) - y_(1) )^(2) }`

`d = \sqrt{(-2 - 2) )^(2) +(-1 - 4 )^(2) }`

`d = \sqrt{(-4 )^(2) +(-5 )^(2) }`

`d = √(16 +25 )`

`d = √(41 )`

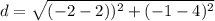
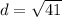
d≈6.40