Question

Given triangle VWX ~ triangle ZYX, find VW

Answer 1

The length of side VW is equal to 32.4 units.

When two triangles are similar, the corresponding sides are in proportion. The ratio of the lengths of corresponding sides in similar triangles is equal. Therefore, for the similar triangles VWX and ZYX:

`(YZ)/(WV) = (XY)/(XW)`

`(18)/(WV) = (27-12)/(27)`

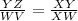
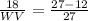
VW=32.4

In similar triangles VWX and ZYX, the corresponding sides are in proportion. The ratio of YZ to WV equals the ratio of XY to XW.

Applying this to the given values, 18 (the length of YZ) divided by WV is equivalent to the difference between 27 (the length of XY) and 12, divided by 27.

Solving for WV, we find that WV is equal to 32.4. This demonstrates the principle that in similar triangles, corresponding sides maintain a consistent ratio, facilitating calculations of unknown side lengths based on the known ratios in similar geometric figures.