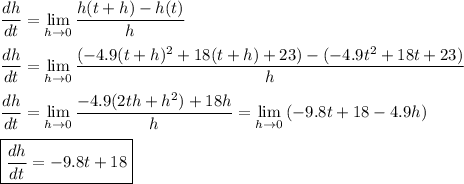9514 1404 393
Answer:
b) -9.8t +18
Explanation:
b) The instantaneous rate of change is the derivative of the height function. The power rule is separately applied to each term, and the results added.
power rule: d/dx(x^n) = nx^(n-1)
Then the derivative is ...
dh/dt = 2(-4.9t^1) +18(1 ·t^0)
dh/dt = -9.8t +18
__
If you haven't been introduced to derivatives as such, then you find the instantaneous rate of change by finding the average rate of change over a vanishing interval.