Question

The weights for 12-month-old males are normally distributed with a mean of 22.6 pounds and a standard deviation of 2.8 pounds. Use z-score table to find the percentage of 12-month-old males who weigh more than 26.8 pounds. round to two decimal places as needed.

Answer 1

The percentage of 12-month-old males who weigh more than 26.8 pounds is approximately 13.59%.

To find the percentage of 12-month-old males who weigh more than 26.8 pounds, we can use the z-score table and the given mean and standard deviation of the weights for 12-month-old males.

Calculate the z-score for 26.8 pounds:

`Z-score: $(X - \mu)/(\sigma)$`

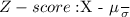
Where X is the weight (26.8 pounds), µ is the mean (22.6 pounds), and σ is the standard deviation (2.8 pounds).

`Z-score: $(26.8 - 22.6)/(2.8) \approx 1.16$`

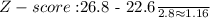
Find the percentage of 12-month-old males with a z-score greater than 1.16 using a z-score table or calculator.

Since we don't have a z-score table handy, we can use a standard normal distribution table (also known as a cumulative distribution function table) for the normal distribution with a mean of 0 and a standard deviation of 1.

Using a standard normal distribution table, we can find that the percentage of 12-month-old males with a z-score greater than 1.16 is approximately 13.59%.

The percentage of 12-month-old males who weigh more than 26.8 pounds is approximately 13.59%.